Skip to contents

Parametric and non-parametric stability statistics

Tiago Olivoto

2024-12-13

Source: vignettes/vignettes_stability.Rmd
vignettes_stability.Rmd

Getting started

In this section, we will use the data in data_ge and data_ge2. For more information see ?data_ge and ?data_ge2, respectively. Other data sets can be used provided that the following columns are in the data_ge: environment, genotype, block/replicate and response variable(s).

See the section Rendering engine to know how HTML tables were generated.

Genotype-environment performance

The function ge_plot() may be used to visualize the genotype’s performance across the environments.

library(metan)
a <- ge_plot(data_ge, ENV, GEN, GY)
b <- ge_plot(data_ge, ENV, GEN, GY) + ggplot2::coord_flip()
arrange_ggplot(a, b, tag_levels = "a")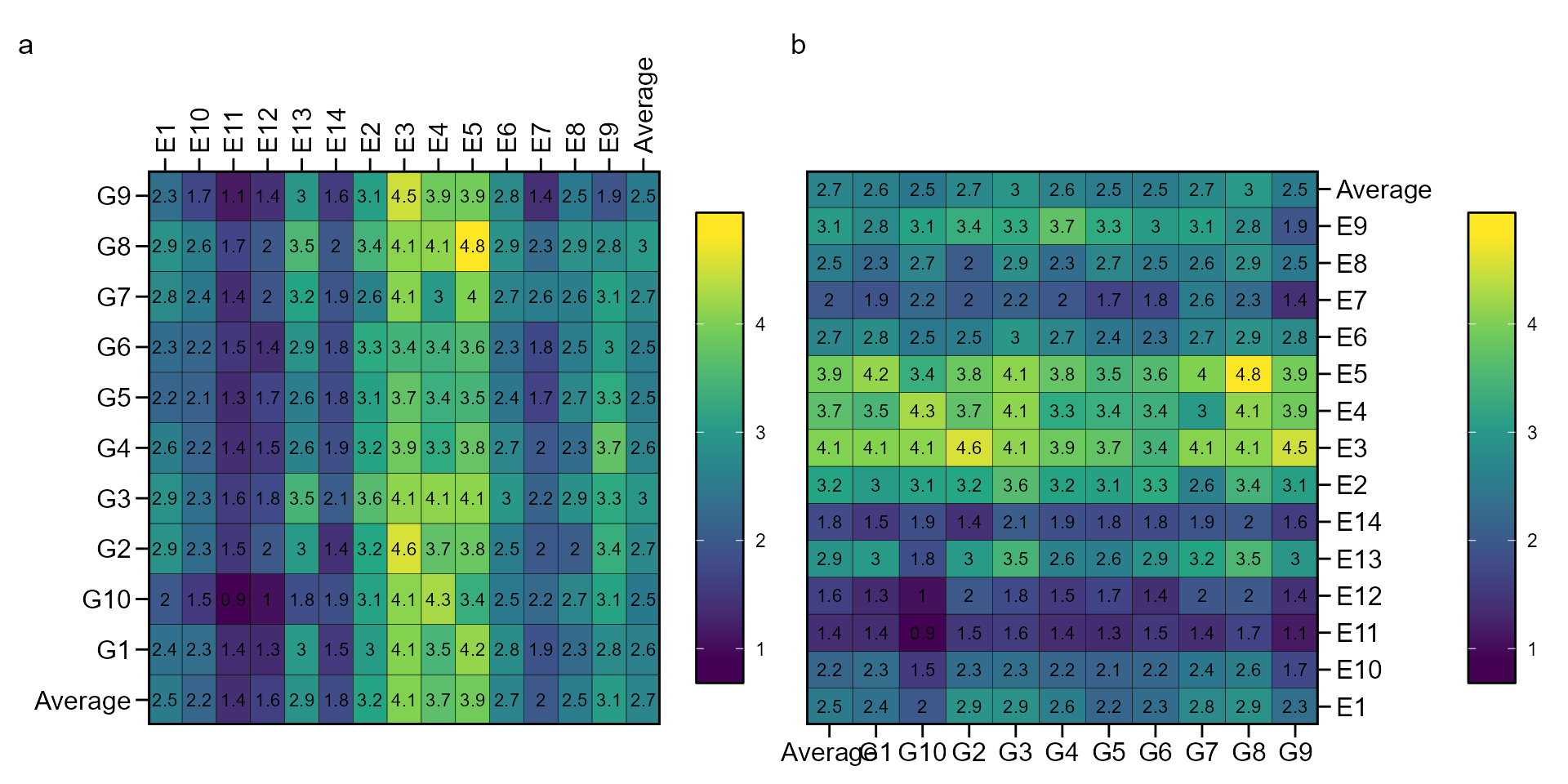

To identify the winner genotype within each environment, we can use the function ge_winners().

ge_winners(data_ge2, ENV, GEN, resp = everything()) %>% print_table()

Or get the genotype ranking within each environment.

ge_winners(data_ge2, ENV, GEN, resp = everything(), type = "ranks") %>% 
  print_table()

For more details about the trials, we can use ge_details()

ge_details(data_ge2, ENV, GEN, resp = everything()) %>% 
  print_table()

Within-environment analysis of variance

The function anova_ind() can be used to compute an within-environment analysis of variance. Environment with values in blue had a significant (p < 0.05) genotype effect.

ind <- anova_ind(data_ge, ENV, GEN, REP, GY)
# Evaluating trait GY |============================================| 100% 00:00:00 
print_table(ind$GY$individual)

Genotype-by-environment means

The function make_mat() can be used to produce a two-way table for the genotype-environment means.

make_mat(data_ge, GEN, ENV, GY) %>% print_table(rownames = TRUE)

Genotype-by-environment interaction effects

The function ge_effects() is used to compute the genotype-environment effects.

ge_ef <- ge_effects(data_ge, ENV, GEN, GY)
print_table(ge_ef$GY)

Genotype plus Genotype-by-environment effects

To obtain the genotype plus genotype-environment effects, we can use the argument type = "gge" in the function ge_effects().

gge_ef <- ge_effects(data_ge, ENV, GEN, GY, type = "gge")
print_table(gge_ef$GY)

Clustering tester locations

The function ge_cluster() computes a cluster analysis for grouping environments based on its similarities using an Euclidean distance based on standardized data. Line means are divided by the phenotypic standard error of the relevant environment after its mean has been subtracted. By standardizing the data each environment will have a mean of zero and unit variance, and the effect of variability in phenotypic variance (as well as the mean) should be reduced (Fox and Rosielle 1982).

d1 <- ge_cluster(data_ge, ENV, GEN, GY, nclust = 4)
plot(d1, nclust = 4)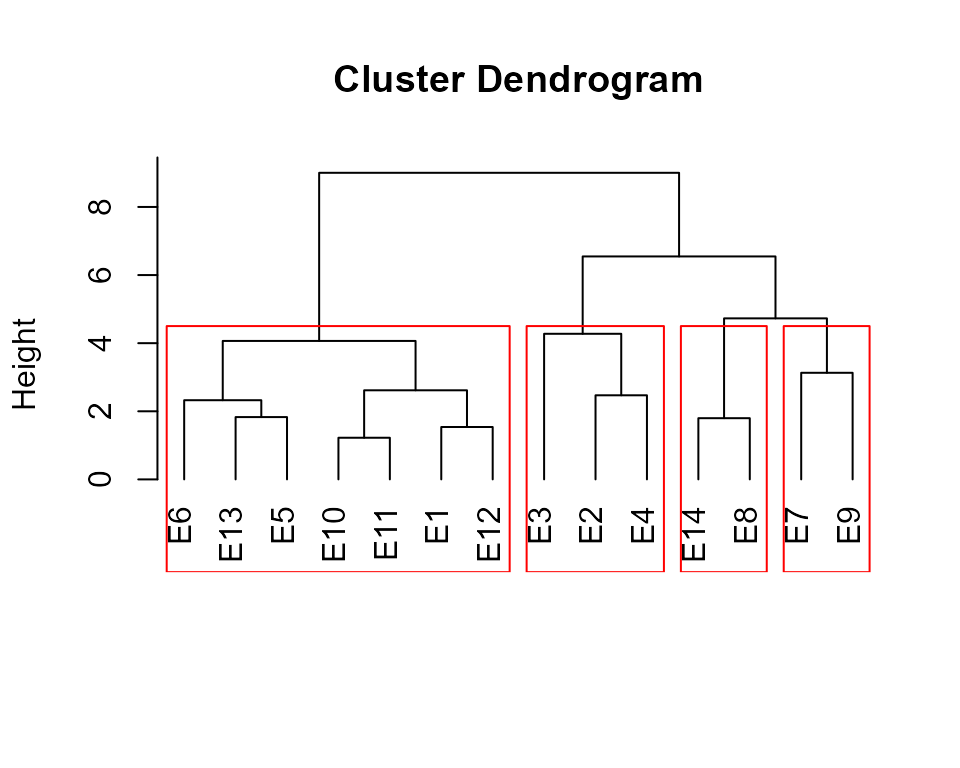

The function env_dissimilarity() computes the dissimilarity between test environment using:

  • The partition of the partition of the mean square of the genotype-environment interaction (MS_GE) into single (S) and complex (C) parts, according to Robertson (1959), where S=12(Q1−Q2)2)S = \frac{1}{2}(\sqrt{Q_1}-\sqrt{Q_2})^2) and C=(1−r)Q1−Q2C = (1-r)\sqrt{Q1-Q2}, being rr the correlation between the genotype’s average in the two environments; and Q1Q_1 and Q2Q_2 the genotype mean square in the environments 1 and 2, respectively

  • The decomposition of the MS_GE, in which the complex part is given by C=(1−r)3×Q1×Q2C = \sqrt{(1-r)^3\times Q1\times Q2}(Cruz and Castoldi 1991).

  • The interaction mean square between genotypes and pairs of environments.

  • The correlation coefficients between genotypes’s average in each pair of environment.

mod <- env_dissimilarity(data_ge, ENV, GEN, REP, GY)
# Evaluating trait Y |=============================================| 100% 00:00:00 
# Pearson's correlation coefficient
print_table(mod$GY$correlation, rownames = TRUE)
# Mean square GxEjj'
print_table(mod$GY$MSGE, rownames = TRUE)
# % Of the single part of MS GxEjj' (Robertson, 1959)
print_table(mod$GY$SPART_RO, rownames = TRUE)
# % Of the complex part of MS GxEjj' (Robertson, 1959)
print_table(mod$GY$CPART_RO, rownames = TRUE)
# % Of the single part of MS GxEjj' (Cruz and Castoldi, 1991)
print_table(mod$GY$SPART_CC, rownames = TRUE)
# % Of the complex part of MS GxEjj' (Cruz and Castoldi, 1991)
print_table(mod$GY$CPART_CC, rownames = TRUE)

To obtain dendrograms based on the above matrix we can use plot(). The dendrograms are based on the hierarchical clustering algorithm UPGMA (Unweighted Pair Group Method using Arithmetic averages).

plot(mod)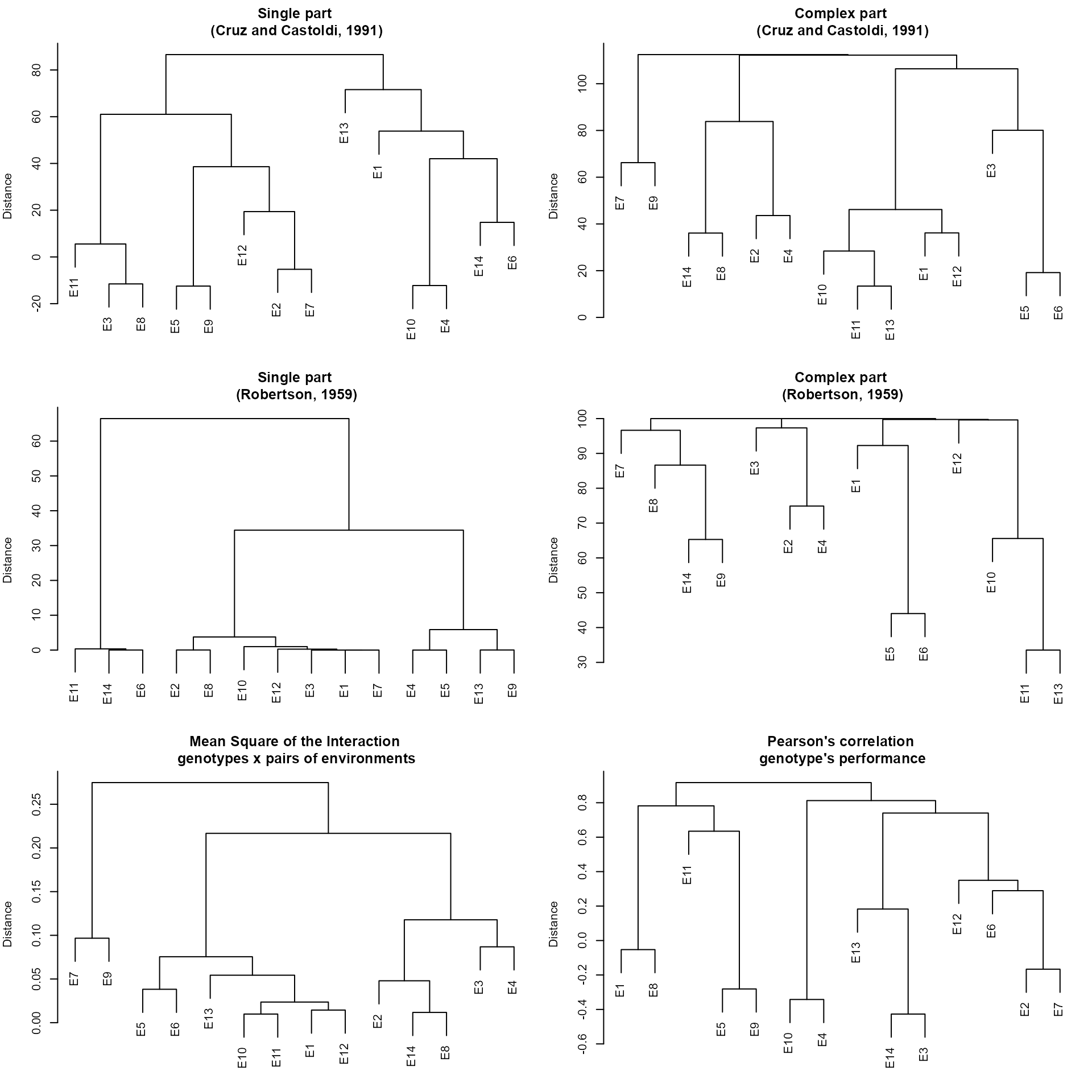

Joint regression analysis

Eberhart and Russell (1966) popularized the regression-based stability analysis. In these procedures, the adaptability and stability analysis is performed by means of adjustments of regression equations where the dependent variable is predicted as a function of an environmental index, according to the following model:

Yij=β0i+β1iIj+δij+ε‾ij \mathop Y\nolimits_{ij} = {\beta _{0i}} + {\beta _{1i}}{I_j} + {\delta _{ij}} + {\bar \varepsilon _{ij}} where β0i{\beta _{0i}} is the grand mean of the genotype i (i = 1, 2, …, I); β1i{\beta _{1i}} is the linear response (slope) of the genotype i to the environmental index; Ij is the environmental index (j = 1, 2, …, e), where Ij=[(y.j/g)−(y../ge)]{I_j} = [(y_{.j}/g)- (y_{..}/ge)], δij{\delta _{ij}} is the deviation from the regression, and ε‾ij{\bar \varepsilon _{ij}} is the experimental error.

The model is fitted with the function ge_reg(). The S3 methods plot() and summary() may be used to explore the fitted model.

reg_model <- ge_reg(data_ge, ENV, GEN, REP, GY)
# Evaluating trait GY |============================================| 100% 00:00:01 
print_table(reg_model$GY$anova)
print_table(reg_model$GY$regression)

Genotypic confidence index

Annicchiarico (1992) proposed a stability method in which the stability parameter is measured by the superiority of the genotype in relation to the average of each environment, according to the following model:

Zij=YijY‾.j×100 {Z_{ij}} = \frac{{{Y_{ij}}}}{{{{\bar Y}_{.j}}}} \times 100 The genotypic confidence index of the genotype i (WiW_i) is then estimated as follows:

Wi=Zi./e−α×sd(Zi.) W_i = Z_{i.}/e - \alpha \times sd(Z_{i.}) Where α\alpha is the quantile of the standard normal distribution at a given probability error (α≈1.64\alpha \approx 1.64 at 0.05). The method is implemented using the function Annicchiarico(). The confidence index is estimated considering all environment, favorable environments (positive index) and unfavorable environments (negative index), as follows:

Computing the index 

ann5 <- Annicchiarico(data_ge, ENV, GEN, REP, GY)
# Evaluating trait GY |============================================| 100% 00:00:00 
ann1 <- Annicchiarico(data_ge, ENV, GEN, REP, GY, prob = 0.01)
# Evaluating trait GY |============================================| 100% 00:00:00

Environment classification 

print_table(ann5$GY$environments)

Index computed with all environments 

print_table(ann5$GY$general)

Superiority index

The function superiority() implements the nonparametric method proposed by Lin and Binns (1988), which considers that a measure of cultivar general superiority for cultivar x location data is defined as the distance mean square between the cultivar’s response and the maximum response averaged over all locations, according to the following model.

Pi=∑j=1n(yij−y.j)2/(2n) P_i = \sum\limits_{j = 1}^n{(y_{ij} - y_{.j})^2/(2n)} where n is the number of environments

Similar then the genotypic confidence index, the superiority index is calculated by all environments, favorable, and unfavorable environments.

super <- superiority(data_ge, ENV, GEN, GY)
# Evaluating trait GY |============================================| 100% 00:00:00 
print_table(super$GY$index)

Environmental stratification

A method that combines stability analysis and environmental stratification using factor analysis was proposed by Murakami and Cruz (2004). This method is implemented with the function ge_factanal(), as follows:

fact <- ge_factanal(data_ge, ENV, GEN, REP, GY)
plot(fact)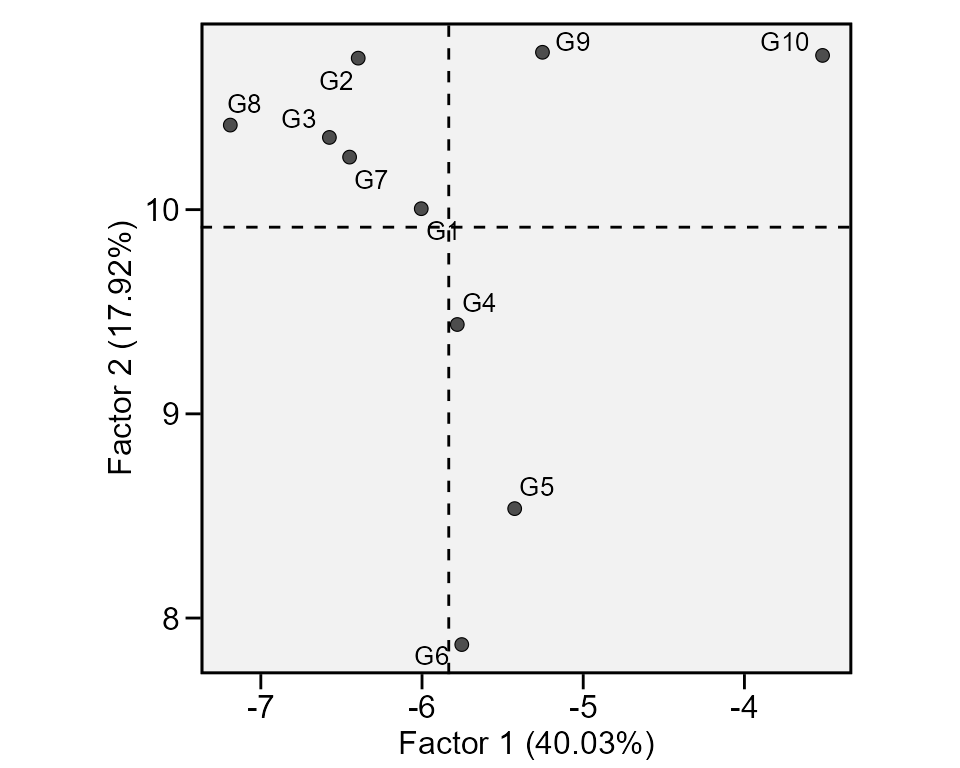

print_table(fact$GY$PCA)
print_table(fact$GY$FA)
print_table(fact$GY$env_strat)

Wrapper function

The easiest way to compute the above-mentioned stability indexes is by using the function ge_stats(). It is a wrapper function that computes all the stability indexes at once. To get the results into a “ready-to-read” file, use get_model_data().

stat_ge <- data_ge2 %>% ge_stats(ENV, GEN, REP, resp = c(EH, PH))
# Evaluating trait EH |======================                      | 50% 00:00:03 Evaluating trait PH |============================================| 100% 00:00:07 
get_model_data(stat_ge, "stats") %>% print_table()
# Class of the model: ge_stats
# Variable extracted: stats
get_model_data(stat_ge, "ranks") %>% print_table(digits = 1)
# Class of the model: ge_stats
# Variable extracted: ranks

It is also possible to obtain the Spearman’s rank correlation between the stability indexes by using corr_stab_ind().

corr_stab_ind(stat_ge)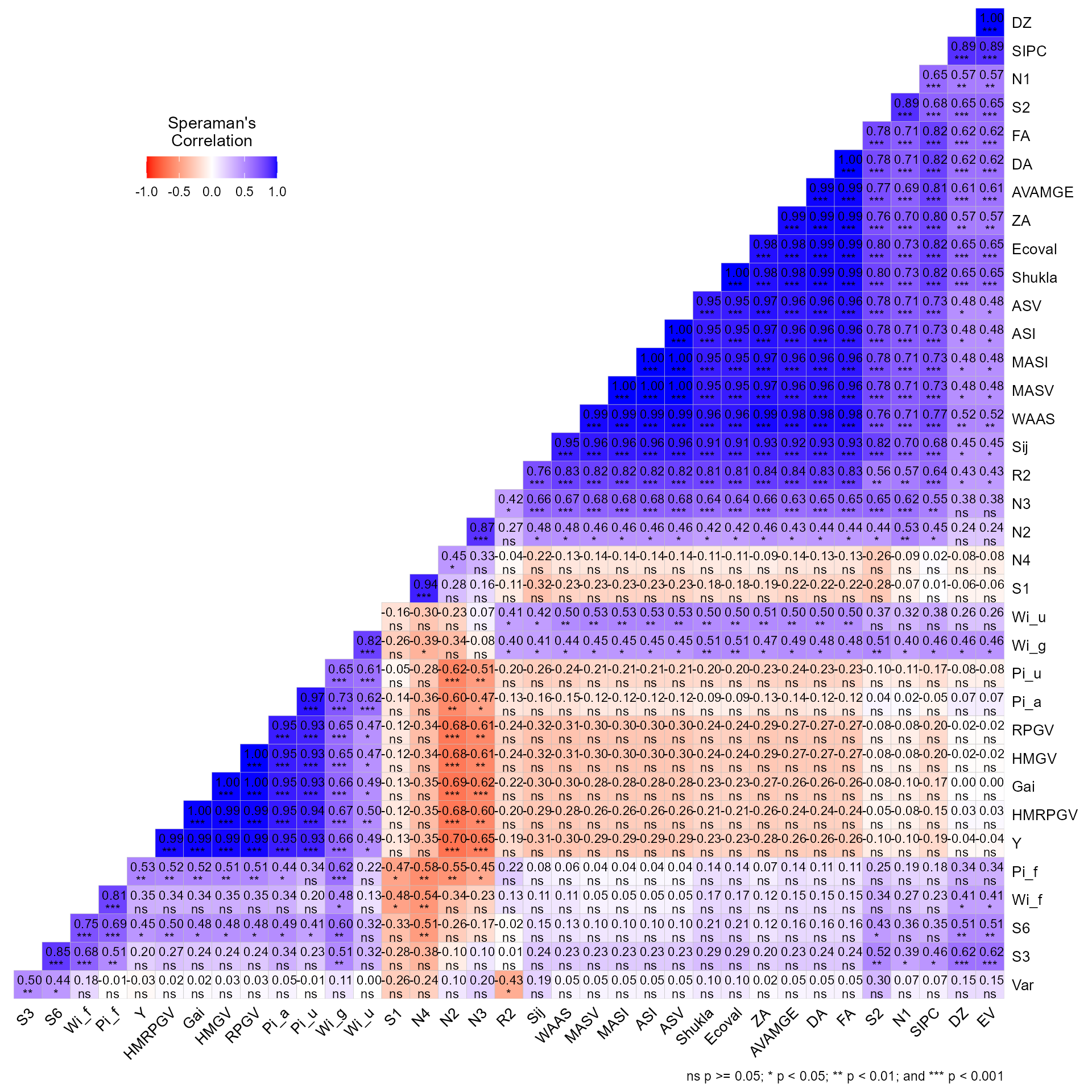

Rendering engine

This vignette was built with pkgdown. All tables were produced with the package DT using the following function.

library(DT) # Used to make the tables
# Function to make HTML tables
print_table <- function(table, rownames = FALSE, digits = 3, ...){
  df <- datatable(table, rownames = rownames, extensions = 'Buttons',
                  options = list(scrollX = TRUE, 
                                 dom = '<<t>Bp>',
                                 buttons = c('copy', 'excel', 'pdf', 'print')), ...)
  num_cols <- c(as.numeric(which(sapply(table, class) == "numeric")))
  if(length(num_cols) > 0){
    formatSignif(df, columns = num_cols, digits = digits)
  } else{
    df
  }
}

References

Annicchiarico, P. 1992. “Cultivar adaptation and recommendation from alfalfa trials in Northern Italy.” Journal of Genetics and Breeding 46: 269–78.
Cruz, C. D., and F. L. Castoldi. 1991. “Decomposição da interação genótipos x ambientes em partes simples e complexa.” Ceres.ufv.br 38: 422–30. http://www.ceres.ufv.br/ojs/index.php/ceres/article/view/2165.
Eberhart, S. A., and W. A. Russell. 1966. “Stability parameters for comparing Varieties.” Crop Science 6 (1): 36–40. https://doi.org/10.2135/cropsci1966.0011183X000600010011x.
Fox, P. N., and A. A. Rosielle. 1982. “Reducing the influence of environmental main-effects on pattern analysis of plant breeding environments.” Euphytica 31 (3): 645–56. https://doi.org/10.1007/BF00039203.
Lin, C. S., and M. R. Binns. 1988. “A superiority measure of cultivar performance for cultivar x location data.” Canadian Journal of Plant Science 68 (1): 193–98. https://doi.org/10.4141/cjps88-018.
Murakami, D. M., and C. D. Cruz. 2004. “Proposal of methodologies for environment stratification and analysis of genotype adaptability.” Crop Breeding and Applied Biotechnology 4 (1): 7–11.
Robertson, A. 1959. Experimental design on the measurement of heritabilities and genetic correlations: biometrical genetics. New York, US: Pergamon.